Spectrograms

The Spectrogram and The Gabor Transform

Summary

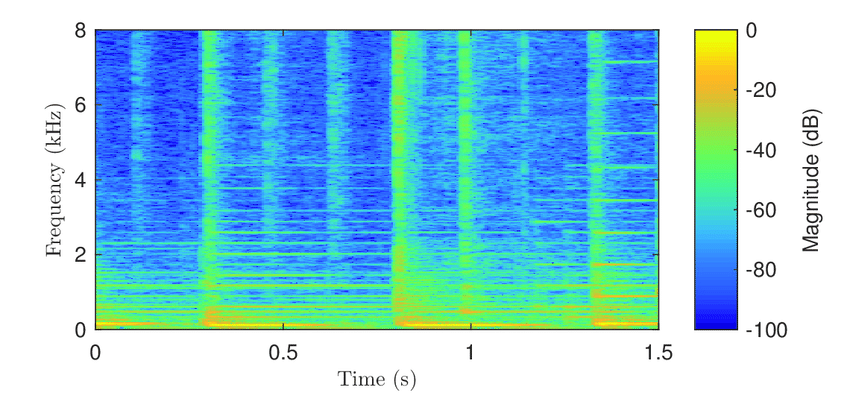
The Gabor transform is used to compute the spectrogram, which shows the frequency content and temporal information of a signal. It is useful for analyzing Brain Activity Signal, EEG, audio signals and classifying sounds.

Gabor Transform

The Gabor transform of a signal ( x(t) ) is defined by this formula:

$G_x(\tau ,\omega )={\int }_{-\infty }^{\infty }x(t)e^{-\pi (t-\tau {)}^2}{e}^{-j\omega t}dt$

In this equation:

• ( x(t) ) is the signal to be transformed.
• The term : $e^{-\pi (t-\tau {)}^2}$represents a Gaussian window function, which gives higher weight to the signal near the time being analyzed.
• The term : $e^{-j\omega t}$ is the Fourier transform, which gives the frequency components of the signal.
• The integral over all time $(-\infty )$ to $(\infty )$ calculates the Fourier transform for each position of the Gaussian window, resulting in a time-frequency analysis.

Highlights

• 🎵 The Gabor transform computes the spectrogram, showing frequency and temporal information of a signal.
• 🎹 The Fourier transform gives frequency components of a signal, but not their timing.
• 📊 The Gabor transform combines frequency and temporal information to create a time-frequency plot.
• 🌊 The spectrogram is useful for classifying sounds, analyzing data, and identifying features in audio signals.
• 🎶 Shazam uses the spectrogram to match peaks in the power spectrum with known songs.
• 🎸 The spectrogram can help classify instruments and even differentiate musicians based on their playing style.
• 🎹 The spectrogram of Beethoven’s sonata reveals the timing and intensity of each note.

Key Insights

• 💡 The Fourier transform provides frequency information, while the Gabor transform combines frequency and temporal information in the spectrogram.
• 💡 The spectrogram is a valuable tool for analyzing audio signals, classifying sounds, and identifying features in data.
• 💡 Shazam uses the spectrogram to match peaks in the power spectrum with known songs, even accounting for speed variations.
• 💡 The spectrogram can be used to classify instruments and differentiate musicians based on playing styles.
• 💡 The Gabor transform and spectrogram allow us to visualize the timing and intensity of notes in musical compositions.
• 💡 The spectrogram is particularly useful for studying time-varying signals that are not perfectly periodic, like audio recordings.
• 💡 Coding the spectrogram and working with time-frequency diagrams can provide further insights into audio signals and their characteristics.